Javascript required
Skip to content Skip to sidebar Skip to footer
Home / Find the Exact Solution to a Fourth Order Pde

Find the Exact Solution to a Fourth Order Pde

Given following inputs,

  • An ordinary differential equation that defines value of dy/dx in the form x and y.
  • Initial value of y, i.e., y(0)

Thus we are given below.
\frac{\mathrm{dy} }{\mathrm{d} x} = f(x, y),y(0)= y_o
The task is to find value of unknown function y at a given point x.
The Runge-Kutta method finds approximate value of y for a given x. Only first order ordinary differential equations can be solved by using the Runge Kutta 4th order method.
Below is the formula used to compute next value yn+1 from previous value yn. The value of n are 0, 1, 2, 3, ….(x – x0)/h. Here h is step height and xn+1 = x0 + h
. Lower step size means more accuracy.
K_1 = hf(x_n, y_n)\\ K_2 = hf(x_n+\frac{h}{2}, y_n+\frac{k_1}{2})\\ K_3 = hf(x_n+\frac{h}{2}, y_n+\frac{k_2}{2})\\ K_4 = hf(x_n+h, y_n+k_3)\\ y_{n+1} = y_n + k_1/6 + k_2/3 + k_3/3 + k_4/6 + O(h^{5})

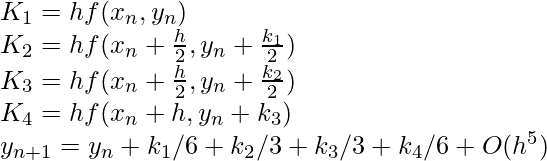
Attention reader! Don't stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.  To complete your preparation from learning a language to DS Algo and many more,  please refer Complete Interview Preparation Course .

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

The formula basically computes next value yn+1 using current yn plus weighted average of four increments.



  • k1 is the increment based on the slope at the beginning of the interval, using y
  • k2 is the increment based on the slope at the midpoint of the interval, using y + hk1/2.
  • k3 is again the increment based on the slope at the midpoint, using using y + hk2/2.
  • k4 is the increment based on the slope at the end of the interval, using y + hk3.

The method is a fourth-order method, meaning that the local truncation error is on the order of O(h5), while the total accumulated error is order O(h4).
Source: https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods

Below is implementation for the above formula.

C

#include<stdio.h>

float dydx( float x, float y)

{

return ((x - y)/2);

}

float rungeKutta( float x0, float y0, float x, float h)

{

int n = ( int )((x - x0) / h);

float k1, k2, k3, k4, k5;

float y = y0;

for ( int i=1; i<=n; i++)

{

k1 = h*dydx(x0, y);

k2 = h*dydx(x0 + 0.5*h, y + 0.5*k1);

k3 = h*dydx(x0 + 0.5*h, y + 0.5*k2);

k4 = h*dydx(x0 + h, y + k3);

y = y + (1.0/6.0)*(k1 + 2*k2 + 2*k3 + k4);;

x0 = x0 + h;

}

return y;

}

int main()

{

float x0 = 0, y = 1, x = 2, h = 0.2;

printf ( "\nThe value of y at x is : %f" ,

rungeKutta(x0, y, x, h));

return 0;

}

Java

import java.io.*;

class differential

{

double dydx( double x, double y)

{

return ((x - y) / 2 );

}

double rungeKutta( double x0, double y0, double x, double h)

{

differential d1 = new differential();

int n = ( int )((x - x0) / h);

double k1, k2, k3, k4, k5;

double y = y0;

for ( int i = 1 ; i <= n; i++)

{

k1 = h * (d1.dydx(x0, y));

k2 = h * (d1.dydx(x0 + 0.5 * h, y + 0.5 * k1));

k3 = h * (d1.dydx(x0 + 0.5 * h, y + 0.5 * k2));

k4 = h * (d1.dydx(x0 + h, y + k3));

y = y + ( 1.0 / 6.0 ) * (k1 + 2 * k2 + 2 * k3 + k4);

x0 = x0 + h;

}

return y;

}

public static void main(String args[])

{

differential d2 = new differential();

double x0 = 0 , y = 1 , x = 2 , h = 0.2 ;

System.out.println( "\nThe value of y at x is : "

+ d2.rungeKutta(x0, y, x, h));

}

}

Python

def dydx(x, y):

return ((x - y) / 2 )

def rungeKutta(x0, y0, x, h):

n = ( int )((x - x0) / h)

y = y0

for i in range ( 1 , n + 1 ):

"Apply Runge Kutta Formulas to find next value of y"

k1 = h * dydx(x0, y)

k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)

k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)

k4 = h * dydx(x0 + h, y + k3)

y = y + ( 1.0 / 6.0 ) * (k1 + 2 * k2 + 2 * k3 + k4)

x0 = x0 + h

return y

x0 = 0

y = 1

x = 2

h = 0.2

print 'The value of y at x is:' , rungeKutta(x0, y, x, h)

C#

using System;

class GFG {

static double dydx( double x, double y)

{

return ((x - y) / 2);

}

static double rungeKutta( double x0,

double y0, double x, double h)

{

int n = ( int )((x - x0) / h);

double k1, k2, k3, k4;

double y = y0;

for ( int i = 1; i <= n; i++)

{

k1 = h * (dydx(x0, y));

k2 = h * (dydx(x0 + 0.5 * h,

y + 0.5 * k1));

k3 = h * (dydx(x0 + 0.5 * h,

y + 0.5 * k2));

k4 = h * (dydx(x0 + h, y + k3));

y = y + (1.0 / 6.0) * (k1 + 2

* k2 + 2 * k3 + k4);

x0 = x0 + h;

}

return y;

}

public static void Main()

{

double x0 = 0, y = 1, x = 2, h = 0.2;

Console.WriteLine( "\nThe value of y"

+ " at x is : "

+ rungeKutta(x0, y, x, h));

}

}

PHP

<?php

function dydx( $x , $y )

{

return (( $x - $y ) / 2);

}

function rungeKutta( $x0 , $y0 , $x , $h )

{

$n = (( $x - $x0 ) / $h );

$k1 ; $k2 ; $k3 ; $k4 ; $k5 ;

$y = $y0 ;

for ( $i = 1; $i <= $n ; $i ++)

{

$k1 = $h * dydx( $x0 , $y );

$k2 = $h * dydx( $x0 + 0.5 * $h ,

$y + 0.5 * $k1 );

$k3 = $h * dydx( $x0 + 0.5 * $h ,

$y + 0.5 * $k2 );

$k4 = $h * dydx( $x0 + $h , $y + $k3 );

$y = $y + (1.0 / 6.0) * ( $k1 + 2 *

$k2 + 2 * $k3 + $k4 );;

$x0 = $x0 + $h ;

}

return $y ;

}

$x0 = 0;

$y = 1;

$x = 2;

$h = 0.2;

echo "The value of y at x is : " ,

rungeKutta( $x0 , $y , $x , $h );

?>

Javascript

<script>

function dydx(x, y)

{

return ((x - y) / 2);

}

function rungeKutta(x0, y0, x, h)

{

let n = parseInt((x - x0) / h, 10);

let k1, k2, k3, k4, k5;

let y = y0;

for (let i = 1; i <= n; i++)

{

k1 = h * dydx(x0, y);

k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1);

k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2);

k4 = h * dydx(x0 + h, y + k3);

y = y + (1 / 6) * (k1 + 2 * k2 +

2 * k3 + k4);;

x0 = x0 + h;

}

return y.toFixed(6);

}

let x0 = 0, y = 1, x = 2, h = 0.2;

document.write( "The value of y at x is : " +

rungeKutta(x0, y, x, h));

</script>

Output: 

The value of y at x is : 1.103639

Time Complexity of above solution is O(n) where n is (x-x0)/h.
Some useful resources for detailed examples and more explanation.
http://w3.gazi.edu.tr/~balbasi/mws_gen_ode_txt_runge4th.pdf
https://www.youtube.com/watch?v=kUcc8vAgoQ0

This article is contributed by Arpit Agarwal. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above


Find the Exact Solution to a Fourth Order Pde

Source: https://www.geeksforgeeks.org/runge-kutta-4th-order-method-solve-differential-equation/